k-Dimensional Trees

Computational geometry is generally concerned with algorithms that solve problems that can be stated in purely geometric terms like: find the smallest polygon which encloses a set of points or construct a data structure to support efficient querying of a set of points. I once interviewed at company that relied on methods from this field. It was during an afternoon one-on-one interview that the k-d tree data structure came up. We, the interviewer and I, were discussing how to find the closest point in a point cloud. At the time, I struggled to find the answer (we were in bonus territory, anyway:)). He explained how one could create a data structure that partitioned the point space into finer and finer cells. And if one keeps track of the relationship between a cell and its constituents, then one can quickly search the space. Essentially, that is what a k-d tree does for point clouds.

k-D dimensional trees are data structures that allow for fast search and querying of point sets. These binary trees have nodes which are k-dimensional points. The tree organizes points by partitioning the point space along each coordinate axis.

Driven to understand this data structure, I coded up a C++ implementation, which you can see on github. Looking at the code: Kdtree class (in kdtree.cpp) represents a k-d tree; main.cpp is essentially a test, that creates a k-d tree with ten randomly generated 3-d points.

{8.40924, 4.11543, 8.10499}, 
{6.50689, 1.3663, 3.43026}, 
{9.7614, 9.8382, 0.672512}, 
{0.113181, 2.22785, 3.46726}, 
{5.23381, 4.69416, 4.74723}, 
{9.74655, 0.191659, 1.20641}, 
{2.8546, 7.32662, 8.51895}, 
{6.21829, 0.779546, 1.82988}, 
{8.83612, 8.70544, 2.40537}, 
{6.50697, 2.70078, 1.93852} 

Which when ploted looks like:

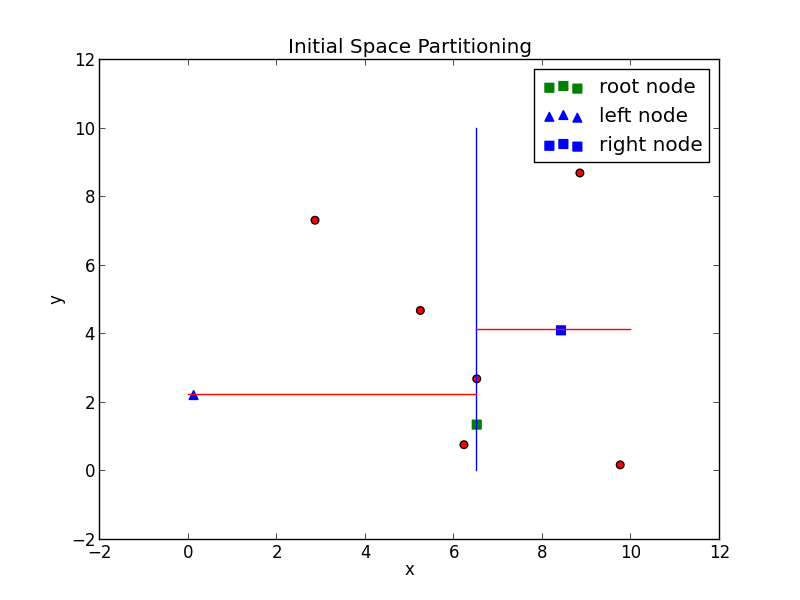
So how does one go about making the tree? Well, we first have to determine which among the ten points will be the root. One could chose a point at random, but doing so won't necessarily yield a balanced tree. The algorithm procedes by recursively partitioning the points along each axis, which in our example are the x,y,z - axes. Beginning with the x-axis, the list of points is sorted with respect the the x-axis, where the median point is choosen to be the root (denote green in the figure below) Points with x-values less than root are then grouped into what I call the left list. Likewise, points with x-values greater than root are grouped into the right list. Each list represents new and smaller point clouds, which in turn are partitioned, but this time not along the x-axis, but the y-axis. Specificaly, the median with respect to the y-axis. The root's children are constructed from the lists' medians--the median of the left list becomes the left child, and the median of the right list becomes the right child.

And the process continues, recursively partition left and right lists, until such lists are empty. The figure below summarizes the first few partitions, and highlights the nodes created.

The algorithm loosely described above in detail:

void Kdtree::_makeTree( Node* head, std::list<Kdtree::vecType>& plist, int depth )
{   
    if( !plist.empty() ) 
    {
        int k = plist.front().size();
        int axis = depth % k;

        std::list<Kdtree::vecType> left_list;
        std::list<Kdtree::vecType> right_list;
        Kdtree::vecType median = Kdtree::findMedian(axis, plist, left_list, right_list); 
        head->data = median;

        Node* left_node = new Node(k);
        Node* right_node = new Node(k);

        Kdtree::_makeTree( left_node, left_list, depth+1);
        if (!left_list.empty()) head->left = left_node;

        Kdtree::_makeTree( right_node, right_list, depth+1);
        if (!right_list.empty()) head->right = right_node;
    }
} 

One of the sweeter parts of this project was getting to use C++11 lambda expressions for median computation. Lambda functions are quick, small, anonymous functions that can be passed around, often as input to other functions. See this write up for more information about C++ lambdas. Check it out:

// Using lambda function here, to define comparison function--parametrized by 'axis'
plist.sort( [&](Kdtree::vecType& a, Kdtree::vecType& b){return a[axis] < b[axis];});

Some background here: std::list has a method for sorting; it takes a comparator function. And in the new C++11 standard there's not need to define the necessary compare function elsewhere, you can instead pass a lambda function defining an ordering. The lambda function shown above is especially nice because it's parameterized by the variable axis, to which it has access, defining a different comparison function for each axis. Otherwise one would have to define separate compare functions for each axis; and where sorting is done and the compare functions are passed--as seen above, plist.sort()--calls for each axis would have to be defined in a switch statement. Lambda saved us a lot of extra coding! Super elegant!!