Losing My Orientation
12 May 2017While trying to grok $SO(3) \cong \mathbb{RP}^3$ and understand various parametrizations of $SO(3)$, I wandered a bit (okay maybe more that litte:) ) and started to think about projective space itself. It is well know that real projective spaces alternate between being orientable and non-orientable, as dimension increases. Specifically odd dimensional projective spaces are orientable but even ones are not. For example, $\mathbb{RP}^1$ and $\mathbb{RP}^3$ are orientable but $\mathbb{RP}^2$ is not.
Jeffery Week’s Shape of Space gives a Flatland inspired explanation of orientations on the projective plane and projective 3-space. It’s a fantastic book and a wonderful example of storytelling as a teaching method. In this note, I want to invoke Week’s style and describe orientations on real projective spaces of any dimension.
Lets start with a low dimensional example, $\mathbb{RP}^2$. There are a few ways to describe the real projective plane: affine plane with points at infinity, as a sphere with antipodes identified, or a disc with boundary antipodes identified. We can’t embed $\mathbb{RP}^2$ in 3-dimensional space so we’re forced to work with patches. So, the disc model will serve our purposes best.
Suppose Pac-Man lives on the real projective plane. He’s hungry and sees food down the road. The boundary of the disc is identified, albeit in a reverse oriented way (note the arrows), so Pac-Man sees no obstruction.
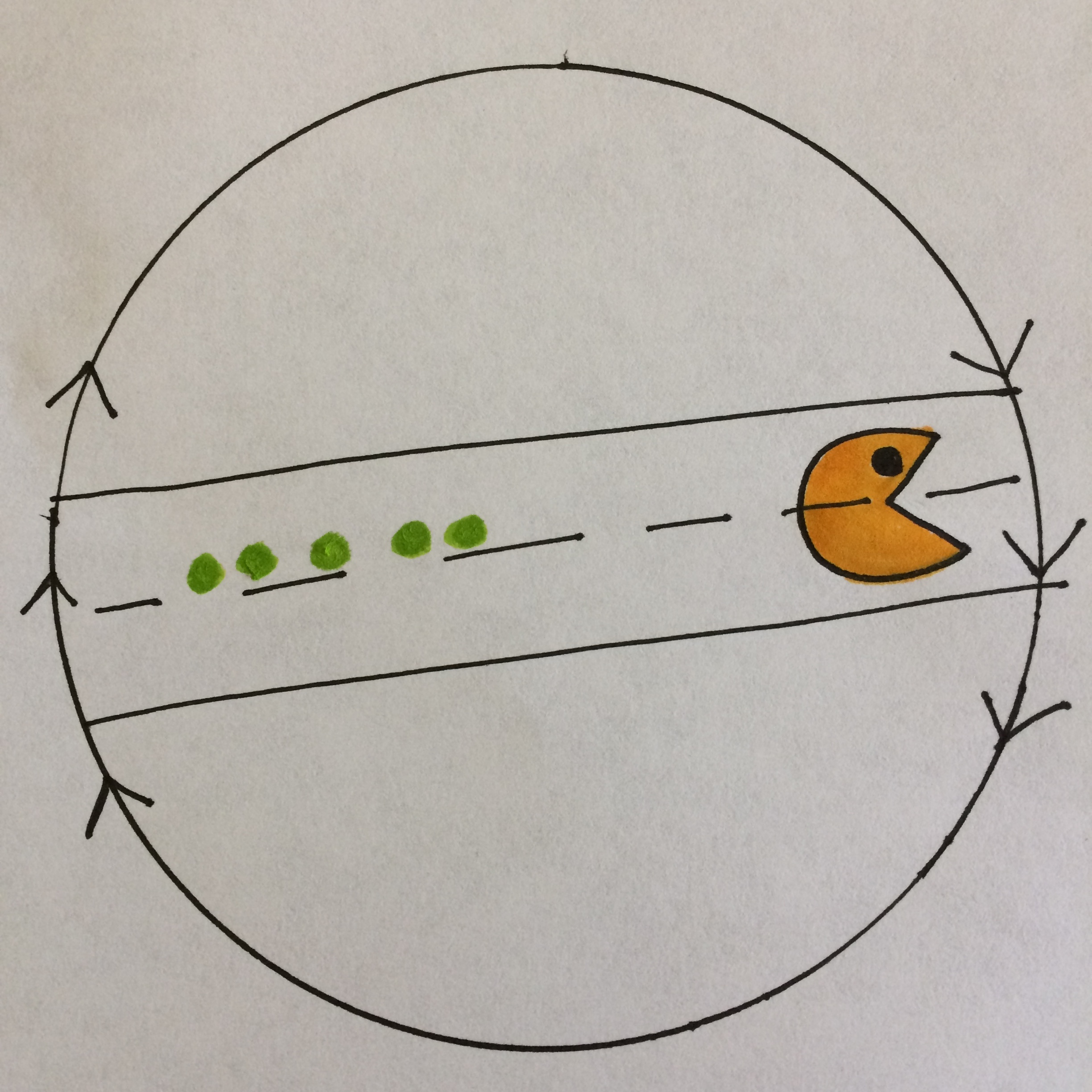
What does Pac-Man look like when he crosses the disc boundary?
Antipodal identification means that as Pac-Man crosses the boundary of the disc, he is flipped about his midline. As he emerges from the left side he appears flipped with his left side in view. Of course in 2-dimensional space there is no sidedness, but we can excise the road with Pac-Man ( after all it is just a Möbius Band! ) and embed it in 3-dimensional space to help us visualize Pac-Man’s journey. Another way to think about it without appealing to a 3-dimensional embedding is to imagine Pac-Man passing through the boundary one vertical strip at a time. Each time a strip hits the boundary it is up-down reversed and then sent to the opposite side. I imagine him emerging from the left side like a image being printed by a dot matrix printer. Each passage of the print head depositing a up-down reversed strip of Pac-Man.
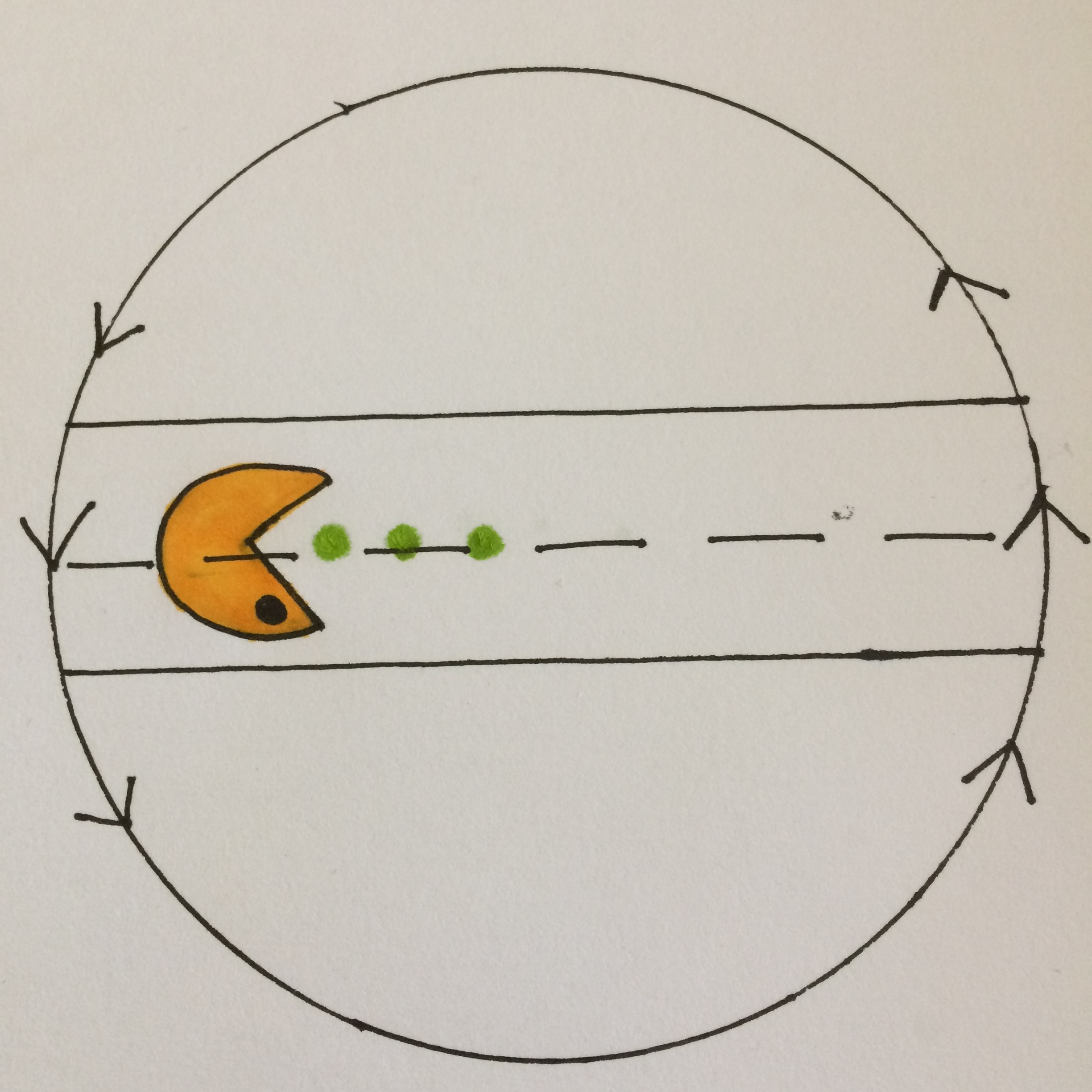
The question remains: Is Pac-Man differently oriented? Imagine an arrow curving the clockwise direction on Pac-Man’s face prior to his passage through the boundary of the disc. That curving arrow is in the counterclockwise direction when he appears from the left; which, to me is a succinct demonstration that Pac-Man’s orientation is reversed.
…So then what is orientation? Well, we’ve seen that Pac-Man is reverse oriented because he’s flipped, once. That could be a definition: one flip. What about two or three, etc.? The boundary identification induces a motion on Pac-Man that leaves his form and shape unchanged. These motions are described by orthogonal groups for continuous objects, like Pac-Man. Though for a more concrete explanation imagine a polygon in 2-dimensions and we only care about how it is rearranged by the topology of the space. These symmetries are described exactly by Dihedral groups; which are composed of flips (reflections) and rotations. It should be clear that rotations are orientation preserving – a clockwise motion rotated remains clockwise. A flip followed by another flip is always a rotation, and rotations form a group. So, we have an answer: an even # of flips preserves orientation, while an odd # of flips reverses orientation.
Lets apply this definition to determine the orientation of $\mathbb{RP}^n$ where $n$ is $3$ or more. We can model $\mathbb{RP}^n$ as a $n$-ball with the boundary antipodally identified. Imagine a boxy Pac-Man floating over a road in $B^n$. Again he sees no boundary because of the identification, nonetheless as he passes through he will be altered somehow.
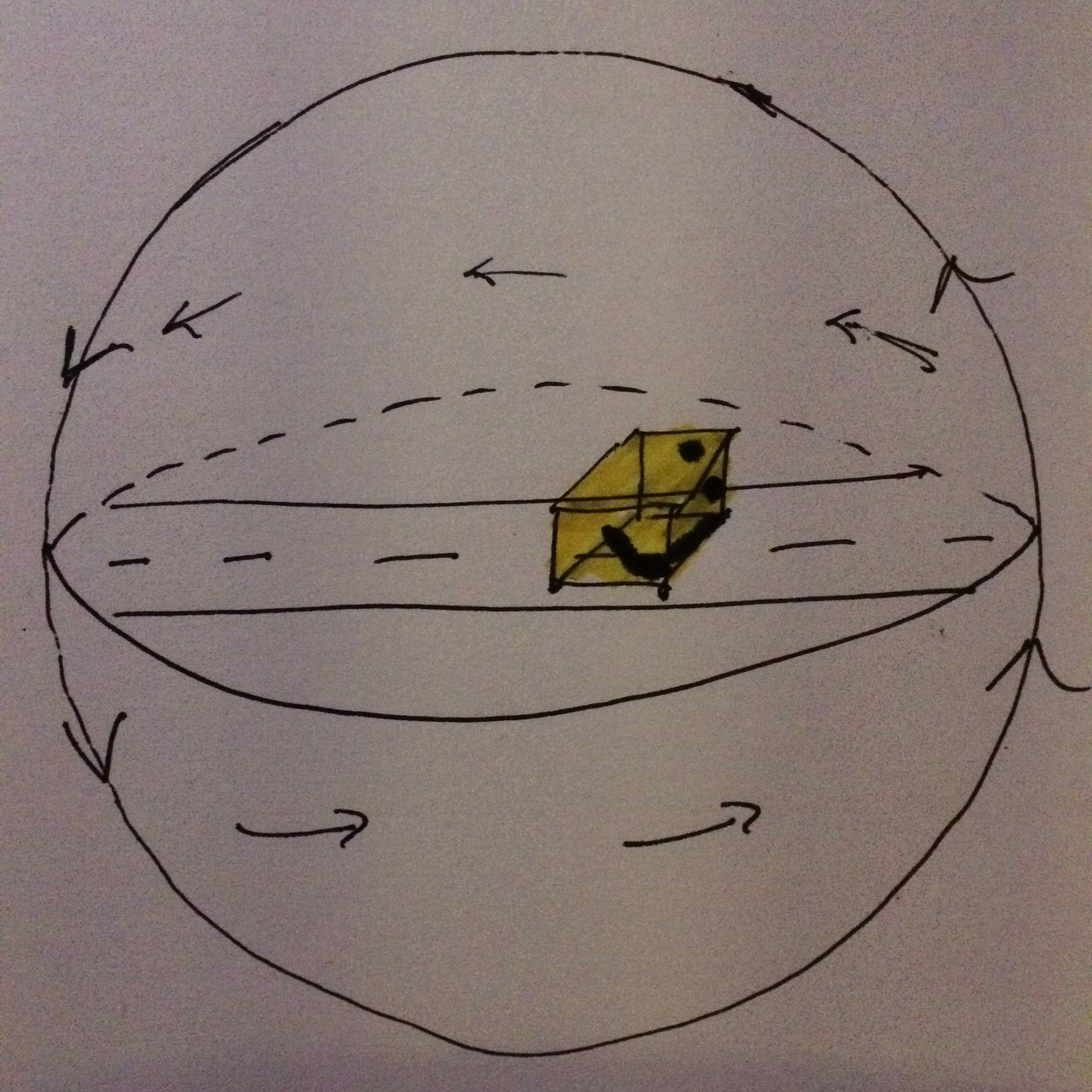
Lets consider $n-1$ dimensional slices of Pac-Man, since the boundary of the ball is a $n-1$-sphere and we can think of Pac-Man passing through the boundary slice by slice. We can imagine the boundary, when viewed heuristically from a $n-1$-dimensional slice, drawn below, as the inside of a sphere. The horizontal axis representing $n-2$ directions and the vertical axis one direction.
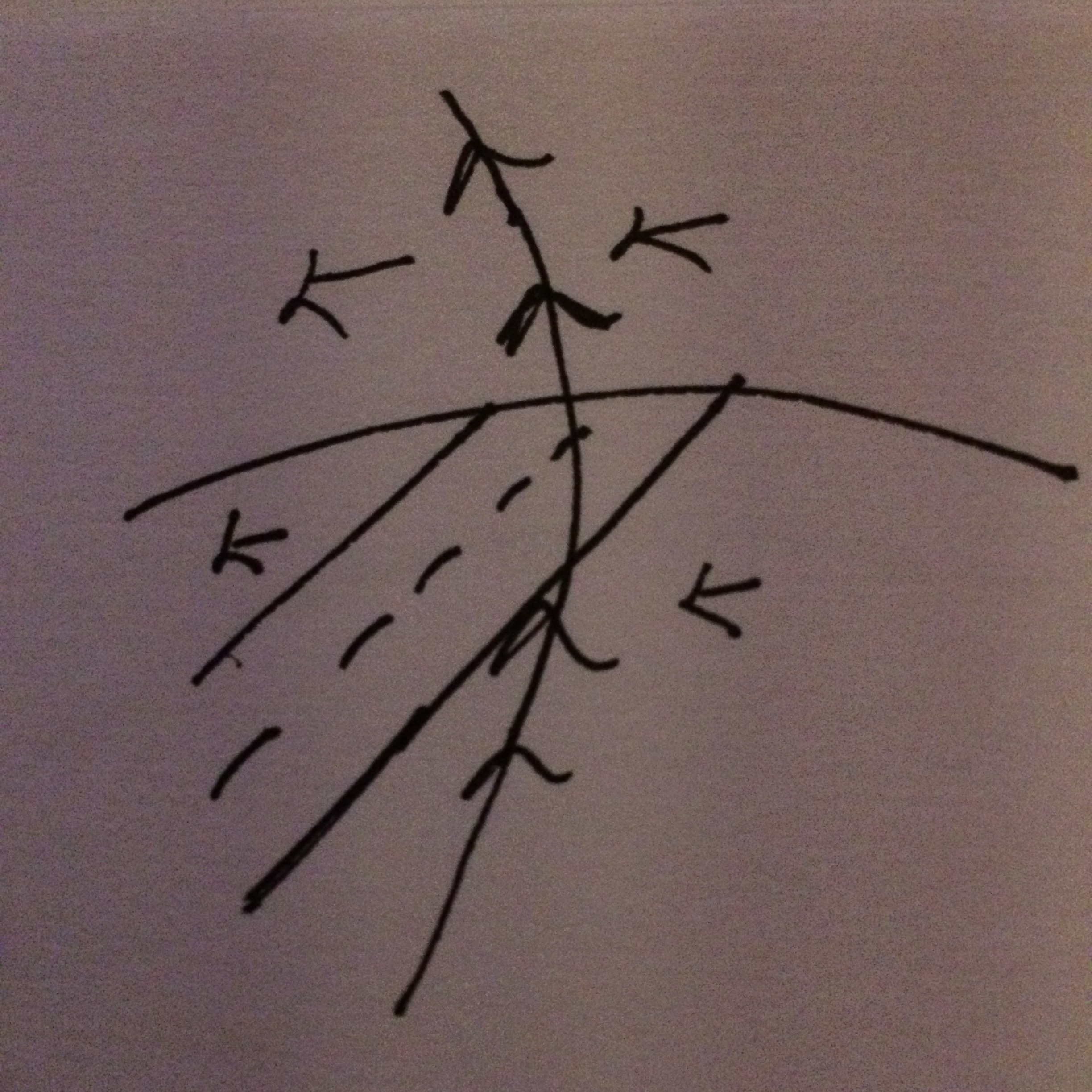
Each slice is flipped $1 + \{ \text{ flips in n-2 directions } \}$ times; a recursive relation–for simplicity let $n$ replace $n-1$; $n$ matches the dimension of the real projective space of interest.
\[\begin{gather*} f(n) = 1 + f(n-1) \quad \text{ where } \quad f(1) = 0 \Longrightarrow \\ f(n) = n-1 \text{ for } n > 0 \end{gather*}\]Orientation is the parity of $f$, so $n-1 \mod 2$ represents orientation. So 3D Pac-Man’s orientation in $\mathbb{RP}^3$ is preserved! And in general
\[\mathbb{RP}^n \text{ is } \left\{ \begin{array}{lr} \text{orientable} & \text{ if } n \mod 2 \equiv 1 \\ \text{non-orientable} & \text{ if } n \mod 2 \equiv 0 \\ \end{array} \right.\]