Average Length of the Longest Arc in $S^1$
13 May 2014Suppose that we draw $n$ points $ a_i \sim Uniform(S^1)$ for $i = 1 \ldots n $. These points determine a partition or set of disjoint arcs of $S^1$. What is the average length of the longest arc? To even measure the $n$ arc lengths, we need an ordering of the
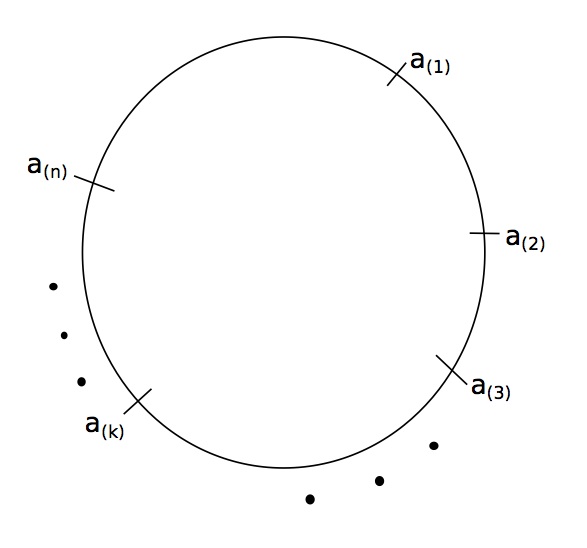
The arc lengths are:
\[\begin{gather*} l_1 = |a_{(2)} - a_{(1)}| \\ \vdots \\ l_{n-1} = |a_{(n)} - a_{(n-1)}| \\ l_n = |a_{(1)} - a_{(n)}| \end{gather*}\]At this point we’d still have to order the arc lengths, to get the longest arc. Ultimately, we need the distribution of
by the inclusion-exclusion principle.
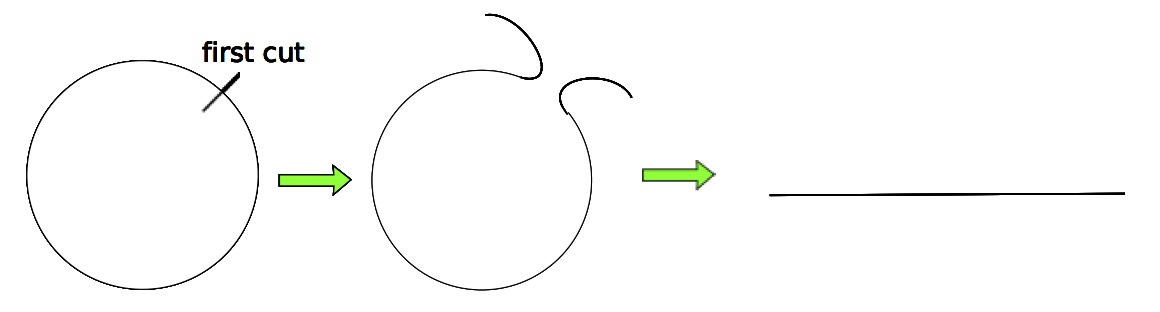
\[\begin{align*} P( l_1 > x, \text{ and } \ldots, \text{ and } l_k > x) & = \text{probability of } n-1 \text{ cuts in a } 2\pi - kx \text{ long arc}\\ & = \left( \frac{2 \pi - kx}{2\pi}\right)^{n-1} \end{align*}\]But why!! The simple graphic below should make this clear. Essentially, we can transform the circle problem to
one on a line, after the first cut: the unit circle problem with $n$ points is the same problem with $n-1$ points
on a $2 \pi$ long line segment. The first cut is superfluous. From there, the argument boils down to recognizing that
each cut is made in segments of total length
Lemma. A Suppose $X \sim p(x)$ is a non-negative random variable, then \[ E[X] = \int^{+\infty}_{0} P(X > x) dx. \]
proof:
Define $F(x) = \int^{x}_{0} p(x) dx = P(X < x)$. Integrating by parts \(\begin{align*} \int^{b}_{0} x p(x) dx & = x \Big\lvert^{b}_{0} \int^{b}_{0}p(x)dx - \int^{b}_{0}F(x)dx \\ & = \int^{b}_{0} dx \int^{b}_{0}p(x)dx - \int^{b}_{0}F(x)dx \\ & = F(b)\int^{b}_{0} dx - \int^{b}_{0}F(x)dx \\ & = F(b)\int^{b}_{0} 1 - F(x)dx \\ & = F(b)\int^{b}_{0} P(X > x)dx \\ \end{align*}\)
Taking the limit as $b \longrightarrow + \infty$ finishes the argument.
q.e.d.
Using the Lemma,
\[\begin{align*} E[l_{(n)}] &= \int^{+\infty}_{0} P(l_{(n)} > x) dx \\ &= \sum^{n}_{k} \binom{n}{k} (-1)^{k-1} \int^{+\infty}_{0}P(l_k > x)dx \\ &= \sum^{n}_{k} \binom{n}{k} (-1)^{k-1} \int^{+\infty}_{0}\left( \frac{2 \pi - kx}{2\pi}\right)^{n-1}dx \\ \end{align*}\]Focusing on the integral, set $u = \frac{2\pi - kx}{2\pi}$,
\[\frac{2 \pi - kx}{2\pi} \geq 0 \quad \Longrightarrow \quad \frac{2\pi}{k} \geq x\] \[\begin{align*} \int^{+\infty}_{0}\left( \frac{2 \pi - kx}{2\pi}\right)^{n-1}dx &= \int^{\frac{2\pi}{k}}_{0}\left( \frac{2 \pi - kx}{2\pi}\right)^{n-1}dx\\ &= \frac{2\pi}{-k}\int^{u(\frac{2\pi}{k})}_{u(0)} u^{n-1}du\\ &= \frac{2\pi}{k}\int^{1}_{0} u^{n-1}du\\ &= \frac{2\pi}{kn} \end{align*}\]Substituting back into the formula,
\[\begin{align*} E[l_{(n)}] &= \frac{2\pi}{n} \sum^{n}_{k} \binom{n}{k} \frac{(-1)^{k-1}}{k} \\ &= \frac{2\pi}{n} \sum^{n}_{k} \frac{1}{k}. \end{align*}\]The last step applies a known binomial sum identity.
Awesome! We have an answer! But is it right? Lets check our work, by generating the empirical distribution of max-segment lengths. I wrote up some code to do this.
In [16]: data = array([ MaxArc(10) for x in range(10000)])
In [17]: data.mean()
Out[17]: 1.8404203486925401
In [18]: 2 * pi * harmonic(10)/10
Out[18]: 1.8403250298528779
Both sample mean and true mean are within a few thousands of each other, which I think validates the analysis above. I took $N = 10$, but other choices will yield similar results.
