30 Dec 2017
3D medical images in the NifTI format store data from MRI acquisitions of some anatomy, like a human brain or heart. When I was a postdoc @Penn my lab was primarily interested in studying brains. Each image associates grayscale values ( in the simplest case ) to discrete coordinates $(i,j,k)$, which describe voxel locations. And for reasons best explained by NifTI FAQ it’s useful/important to align the acquired image to some other coordinate system. This alignment is stored in the image header, as a rigid motion plus an offset. Here’s a bit of NifTI documentation motivating the need to keep the alignment.
This method can also be used to represent "aligned"
coordinates, which would typically result from some post-acquisition
alignment of the volume to a standard orientation (e.g., the same
subject on another day, or a rigid rotation to true anatomical
orientation from the tilted position of the subject in the scanner).
The NifTI standard allows for orientation reversing transforms, but in this post I focus on proper rotations. These rigid motions must preserve volume and orientation; rigidity necessitates linearity. Being a geometric property, volume is preserved when this linear transformation is an isometry; which is to say, for some matrix $A$, $A A^T = I$. Moreover, orientation is preserved when $\det(A) > 0$. The intersection of all these requirements is the group of 3D rotations, usually referred to as the special orthogonal group,
... read more
30 Jun 2017
While learning about Voronoi diagrams from Computational Geometry, I had trouble justifying a single statement from a proof regarding the complexity ( as a function of $n$ sites ) of Voronoi diagrams. For completeness I’ll restate the theorem here.
Theorem. For $n \geq 3$, the number of vertices in the Voronoi diagram of a set of $n$ point sites in the plane is at most $2n-5$ and the number of edges is at most $3n-6$.
To establish the stated bounds, the proof hinges on the constancy of the Euler’s characteristic of graphs (that embed in $S^2$) and every vertex in the Voronoi diagram has degree at least three. Really? At the point in the proof when this fact is invoked we know that all the $n$ sites are not colinear; so given any pair of sites there’s a third site that does not lie on the line passing through them. Three points induce a vertex. But why?? Voronoi vertices have a specific meaning/interpretation; they are equidistant from sites, which means that a Voronoi vertex is the center of circle that passes through at least three sites.
... read more
06 Jun 2017
In a post a few years ago I discussed primality testing. For some reason I thought I described the basic prime number sieve (I’m pretty sure there is only one) there, but apparently I didn’t. No worries. The prime number sieve solves a different problem; that of generating a list of the first $N$ primes. One could use a primality testing method to do this as well; namely filter a list of numbers with the primality test as a predicate; but sieve based methods are faster and conceptually much easier.
The prime number sieve iteratively filters out all the composite numbers, with the caveat that the leading number in the input is a prime. For \(\{ 2,3,4,5,6,7,8,9,10 \}\), we put aside $2$, the smallest number, and filter out all multiples of $2$; then put aside $3$ and filter out multiples of $3$, and so on. This process, shown below as a decreasing sequence, terminates with a set of primes.
... read more
12 May 2017
While trying to grok $SO(3) \cong \mathbb{RP}^3$ and understand various parametrizations of $SO(3)$, I wandered a bit (okay maybe more that litte:) ) and started to think about projective space itself. It is well know that real projective spaces alternate between being orientable and non-orientable, as dimension increases. Specifically odd dimensional projective spaces are orientable but even ones are not. For example, $\mathbb{RP}^1$ and $\mathbb{RP}^3$ are orientable but $\mathbb{RP}^2$ is not.
Jeffery Week’s Shape of Space gives a Flatland inspired explanation of orientations on the projective plane and projective 3-space. It’s a fantastic book and a wonderful example of storytelling as a teaching method. In this note, I want to invoke Week’s style and describe orientations on real projective spaces of any dimension.
... read more
11 Jun 2016
Lately I’ve been thinking about the content of my high school mathematics courses. In my college algebra and trigonmetry class we were introduced to proofs by induction–of all things–somewhere towards the end of my junior year. An important proof technique, for sure. However, the combinatorial expressions they were applied to, like the sum of first $N$ natural numbers, seemed miraculous. Proof by induction is fairly straight forward. But how does one even guess at a closed formula for such expressions? I remember the teacher saying something to the effect “you need to be smart”. I suppose so, but we can actually construct the closed form of the sum of the first $N$ natural numbers.
... read more
13 May 2014
Suppose that we draw $n$ points $ a_i \sim Uniform(S^1)$ for $i = 1 \ldots n $. These points determine a partition or set of disjoint arcs of $S^1$. What is the average length of the longest arc? To even measure the $n$ arc lengths, we need an ordering of the $\{ a_i \}$ , $a_{(1)}, \ldots, a_{(N)} $.
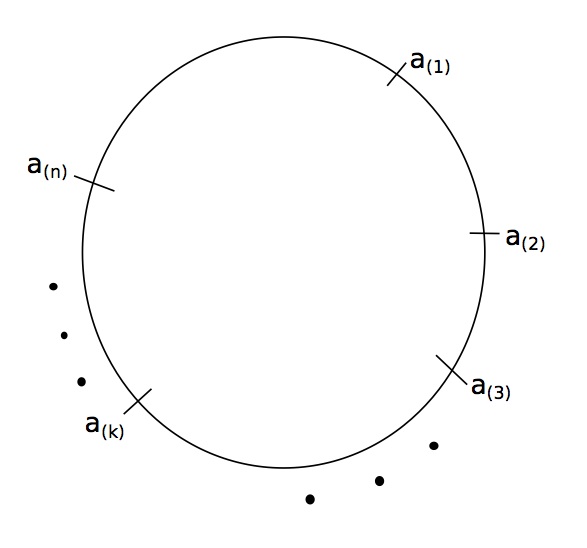
The arc lengths are:
... read more
20 Apr 2014
Awhile ago I was asked how to determine if an integer is prime, which is an important problem. Much of today’s internet security relies on prime numbers–for generating public & private encryption keys. There are other uses too. So, labeling a number prime is well studied. What I want to do in this post is to cover basic algorithms, which rely on testing divisibility of a given number among a list of possible divisors–a search space; and if none divide, the number is prime. By investigating the relationship between a number and its divisors we can reduce the space of possible divisors, and write down a nice sub-linear primality testing algorithm.
Following first principles, an integer $N$ is prime if $\exists a < N$ so that $a\ |\ N$. We could then simply try dividing $N$ by all numbers less than $N$. Here’s our version $0$ algorithm:
... read more
14 Oct 2013
Counting problems abound in mathematics. Often, they are easy to state, but hard to solve. Being easy to understand is what makes them so attractive, and that much more vexing when one gets stuck trying to solve them. Here’s a matrix counting problem I recently encountered.
Problem:
How many $N$ by $N$ matrices with entries $ 0 $ or $1$, and odd row and column sums, are there?
What do these matrices look like? Let $A = [a_{ij}]$. For example
... read more

