Losing My Orientation

While trying to grok $SO(3) \cong \mathbb{RP}^3$ and understand various parametrizations of $SO(3)$, I wandered a bit (okay maybe more that litte:) ) and started to think about projective space itself. It is well know that real projective spaces alternate between being orientable and non-orientable, as dimension increases. Specifically odd dimensional projective spaces are orientable but even ones are not. For example, $\mathbb{RP}^1$ and $\mathbb{RP}^3$ are orientable but $\mathbb{RP}^2$ is not.

Jeffery Week’s Shape of Space gives a Flatland inspired explanation of orientations on the projective plane and projective 3-space. It’s a fantastic book and a wonderful example of storytelling as a teaching method. In this note, I want to invoke Week’s style and describe orientations on real projective spaces of any dimension. ... read more

Sum of the First $N$ Natural Numbers

Lately I’ve been thinking about the content of my high school mathematics courses. In my college algebra and trigonmetry class we were introduced to proofs by induction–of all things–somewhere towards the end of my junior year. An important proof technique, for sure. However, the combinatorial expressions they were applied to, like the sum of first $N$ natural numbers, seemed miraculous. Proof by induction is fairly straight forward. But how does one even guess at a closed formula for such expressions? I remember the teacher saying something to the effect “you need to be smart”. I suppose so, but we can actually construct the closed form of the sum of the first $N$ natural numbers. ... read more

Average Length of the Longest Arc in $S^1$

Suppose that we draw $n$ points $ a_i \sim Uniform(S^1)$ for $i = 1 \ldots n $. These points determine a partition or set of disjoint arcs of $S^1$. What is the average length of the longest arc? To even measure the $n$ arc lengths, we need an ordering of the $\{ a_i \}$ , $a_{(1)}, \ldots, a_{(N)} $.

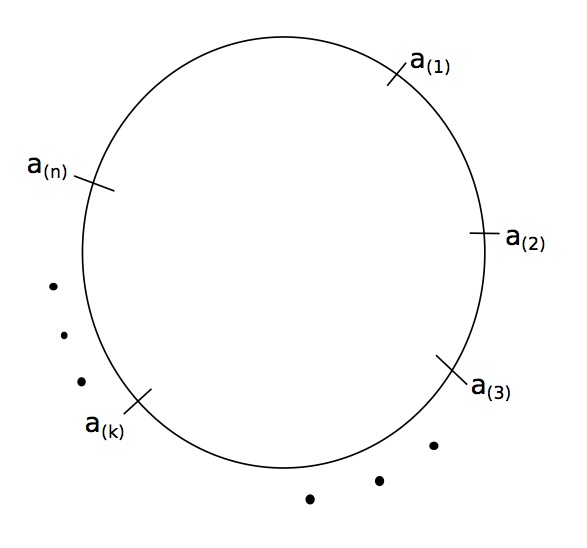
The arc lengths are: ... read more

Super Simple Primality Testing

Awhile ago I was asked how to determine if an integer is prime, which is an important problem. Much of today’s internet security relies on prime numbers–for generating public & private encryption keys. There are other uses too. So, labeling a number prime is well studied. What I want to do in this post is to cover basic algorithms, which rely on testing divisibility of a given number among a list of possible divisors–a search space; and if none divide, the number is prime. By investigating the relationship between a number and its divisors we can reduce the space of possible divisors, and write down a nice sub-linear primality testing algorithm.

Following first principles, an integer $N$ is prime if $\exists a < N$ so that $a\ |\ N$. We could then simply try dividing $N$ by all numbers less than $N$. Here’s our version $0$ algorithm: ... read more

Counting Matrices

Counting problems abound in mathematics. Often, they are easy to state, but hard to solve. Being easy to understand is what makes them so attractive, and that much more vexing when one gets stuck trying to solve them. Here’s a matrix counting problem I recently encountered.

Problem:

How many $N$ by $N$ matrices with entries $ 0 $ or $1$, and odd row and column sums, are there?

What do these matrices look like? Let $A = [a_{ij}]$. For example ... read more

k-Dimensional Trees

Computational geometry is generally concerned with algorithms that solve problems that can be stated in purely geometric terms like: find the smallest polygon which encloses a set of points or construct a data structure to support efficient querying of a set of points. I once interviewed at company that relied on methods from this field. It was during an afternoon one-on-one interview that the k-d tree data structure came up. We, the interviewer and I, were discussing how to find the closest point in a point cloud. At the time, I struggled to find the answer (we were in bonus territory, anyway:)). He explained how one could create a data structure that partitioned the point space into finer and finer cells. And if one keeps track of the relationship between a cell and its constituents, then one can quickly search the space. Essentially, that is what a k-d tree does for point clouds.

k-D dimensional trees are data structures that allow for fast search and querying of point sets. These binary trees have nodes which are k-dimensional points. The tree organizes points by partitioning the point space along each coordinate axis.

... read more